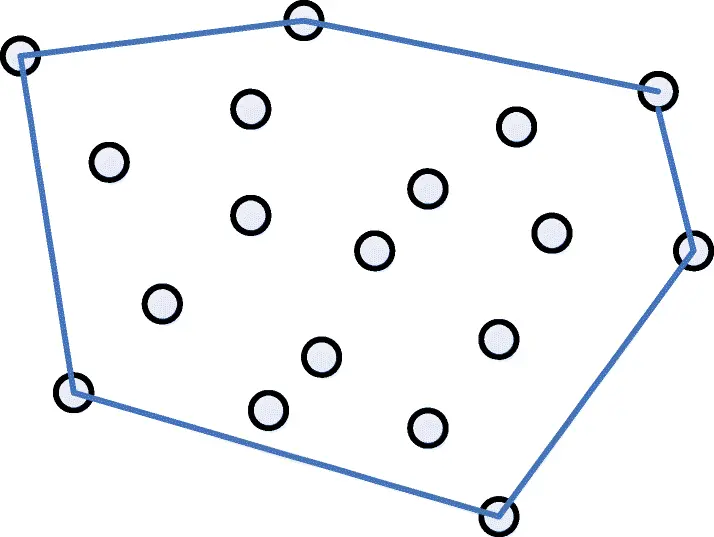
In the Programming Languages course, my exam involved reimplementing the Convex Hull algorithm using Prolog. The goal was to understand the algorithm thoroughly and effectively serialize it in Prolog, a logic programming language that emphasizes declarative coding paradigms 😍. For the same course, a few months earlier, I re-implemented the Little Man Computer, also with Prolog.

The convex hull algorithm is particularly useful in robotics for tasks like pathfinding and obstacle avoidance, where a robot needs to navigate through a set of points while minimizing the boundary path.

🎯 Objectives and Challenges

The primary objective of the project was to implement the Convex Hull algorithm, specifically using Graham's Scan method, in Prolog. This required a deep understanding of both the algorithm and the syntax and features of Prolog. One of the significant challenges was learning how to express the algorithm's logic within Prolog's unique paradigm, which involved predicates and logical inferences rather than conventional control structures.

🚀 Approach and Implementation

I started by finding the point with the lowest Y-coordinate, which served as the reference for the rest of the algorithm. Then, I sorted the points based on their polar angle with this reference point. The core of the implementation involved the graham_scan predicate, which constructed the convex hull by iteratively checking if the sequence of points formed left or right turns, ensuring the convexity of the hull.

Here's a snippet of the key Prolog code:

convexh(Points, CH) :-
    predsort(order_by_yx, Points, [P0 | Ps]),
    retractall(p0(_)),
    assert(p0(P0)),
    sort_point_clockwise_angle(Ps, [P1 | SortedPoints]),
    graham_scan(SortedPoints, [P1, P0], [], [], CHR, _Inner),
    reverse(CHR, CH).

🛠️ Testing and Validation

To ensure the correctness of the implementation, we manually ran several tests with different sets of points. These tests helped us verify that the algorithm correctly identified the convex hull for various configurations of input points. For a visual aid debugging the program I used GeoGebra.

🌟 Outcome and Impact

The successful completion of this project culminated in me receiving the highest grade for the project 🔥. It was a bit painful but overall a fun project to work on! 😆